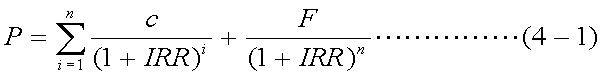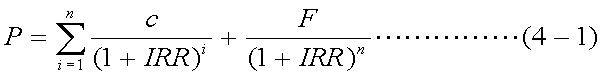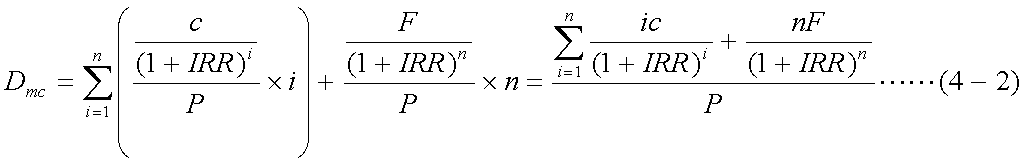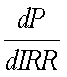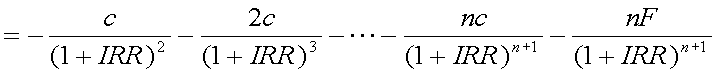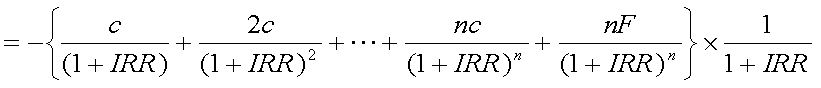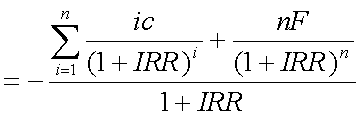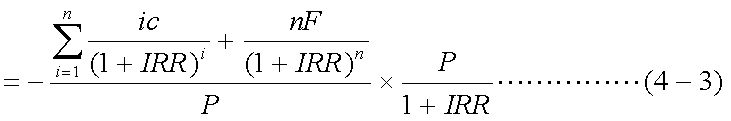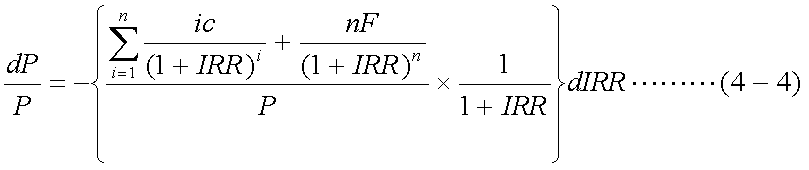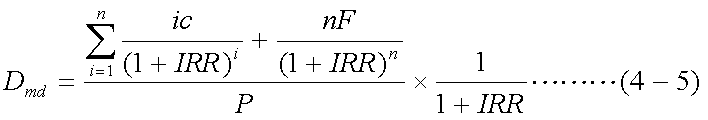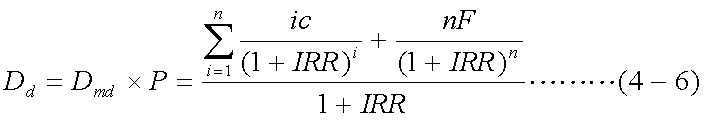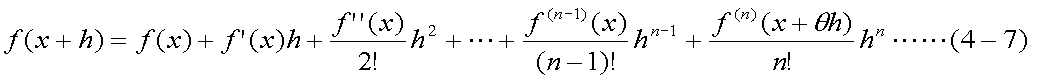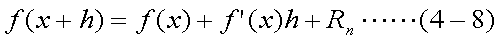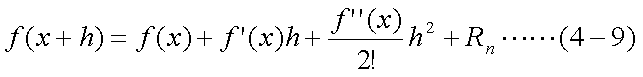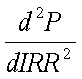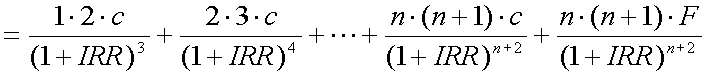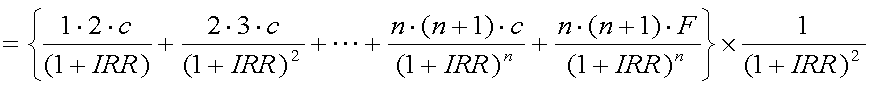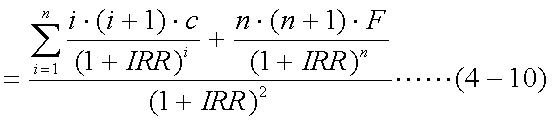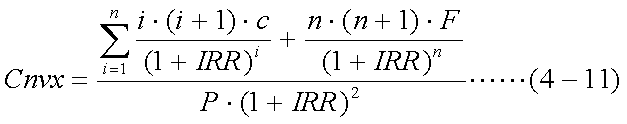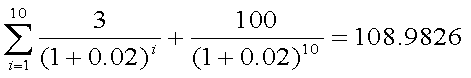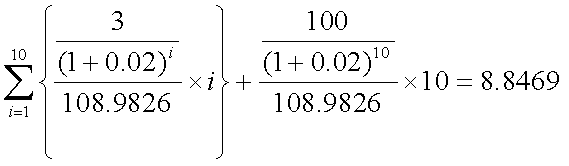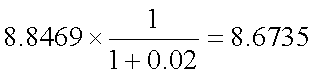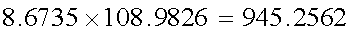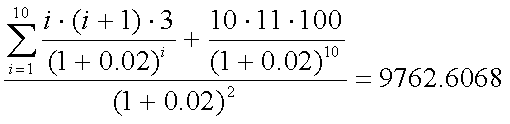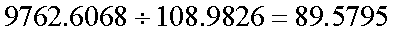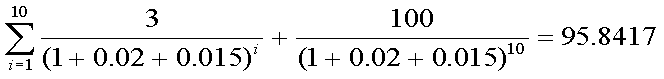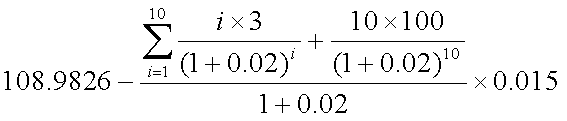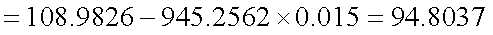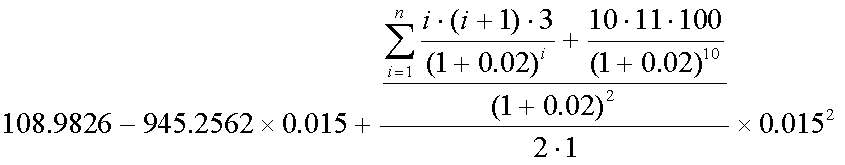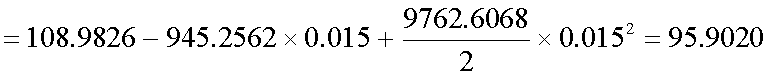1.今回学ぶこと
これまで学んだことから分かるように、債券価格は利回りと密接な関係を持っている。 さらに、債券の利回りは資金の貸し出し金利とも密接な関係を持つものである。 つまり、債券価格は金利によって変動するのであり、債券投資は金利リスクを 負うものであると言うことができる。例えば、金利水準が上昇したとき、これは即ち 現在価格の低下を意味するから、債券価格は低下する。もちろん、償還価格は 変わらないから、償還まで持ちつづければ債券購入当初に期待した収益率は得られる ものの、それは投資期間を通した金利水準に比べて低いものに終わる可能性がある ため、一定の収益獲得機会を損失したと考えることができる。よって、債権投資の 際には、リスク要因である金利と債券価格の関係を分析する必要があり、今回は その主要な指標であるデュレーションについて学ぶ。
2.債券価格と利回りの関係
n年満期で、元本F万円クーポンc%の国債があったとする。 また、利払いは年1回である。この国債の受け渡し日が今日で、現在価格がP 万円であったとすると、1年複利ベース内部収益率(IRR)は、以下の式で表すことが できる。
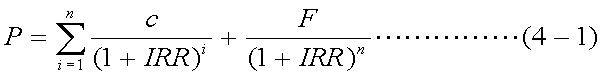 |
式(4-1)について、クーポンを1.9%(前回Newton法での例)、5%、10%とし、 現在価格と内部収益率(正確には、1+IRR)の関係をグラフ化すると、次のように なる。ここで、読み取るべきは以下の4点である。
- 利回り(内部収益率)が上昇すると現在価格は低下し、逆に利回りが低下すると 現在価格が上昇するという一貫した関係がある。つまり、利回りをX軸方向、現在価格 をY軸方向としたとき、グラフは常に左肩上がりである。これは、式(4-1)をIRRで 全微分した1次導関数の値が、常に負となるとこと意味している。
- グラフは常に下に凸である。
- 利回りが低い場合には、利回りの変化に対する価格の変化は大きくなる。
- クーポンが低いものの方が、利回りの変化に対する価格の変化は相対的に大きい。

3.マコーレーのデュレーション
式(4-1)について、IRRを金利水準(即ち、割引率)とすると、マコーレーの デュレーションは、以下の式(4-2)で表される。これは、各キャッシュフローの 現在価値に占める割合を、そのキャッシュフローを受け取るまでの期間に乗ずるもの で、感覚的には、投資額を回収するまでの平均期間を表すものと解釈できる。
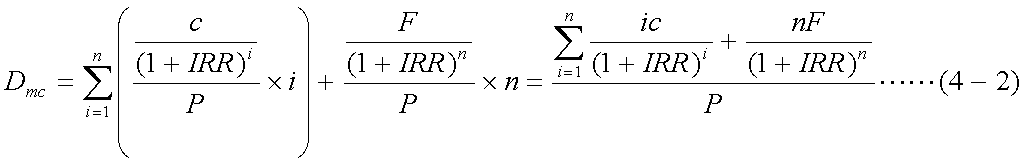
4.修正デュレーション
前項では、マコーレー・デュレーションを、感覚的に投資額回収に必要な平均期間と 捉えたが、それだけでは十分でない。これは、以下のように考えることによって、 金利水準の変動と現在価格の関連を分析することにつながる。 式(4-1)について、金利水準の変化(内部収益率の変化)に対する現在価格の変化を みるためには、これをIRRで全微分して、1次導関数を得ればよい。これは、次の式 (4-3)のように考えられる。
ここで、式(4-3)の第1項がマコーレー・デュレーションであることに留意されたい。 言わばマコーレー・デュレーションについて、金利水準の変化と現在価格との 関連を明確にするための修正を加えたものが、以下で定義する修正デュレーション (モディファイド・デュレーション)である。式(4-3)を、式(4-4)のように変形する。
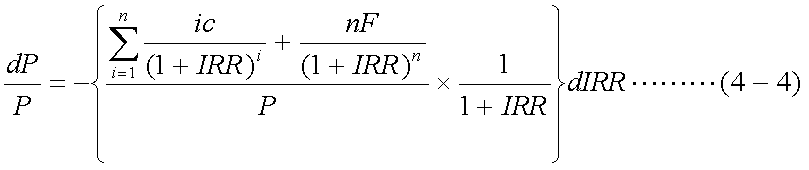
式(4-4)は、金利水準が変化したときの現在価格の変動率を表しており、 修正デュレーションは、以下の式(4-5)で定義される。これは、マコーレー・ デュレーションに、1/(1+IRR)を乗じたものに過ぎないが、金利の変化幅に対する 債券価格の変化率を表すものとなっている(符号は、実際の価格変化方向とは逆) 点を認識しておく必要がある。
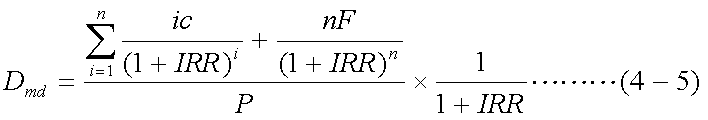
5.ダラー・デュレーション
修正デュレーションは、金利の変化量から現在価格の変化率を 推定するものである。ここで、修正デュレーションに現在価格を乗ずると、 金利の変化量から現在価値の変化量を推定するものに変えることが でき、これをダラー・デュレーション(dollar duration)と呼ぶ。これは、式(4-3)の 符号を逆にしたもの、即ち式(4-1)の1次導関数の値を正にしたものに他ならない。
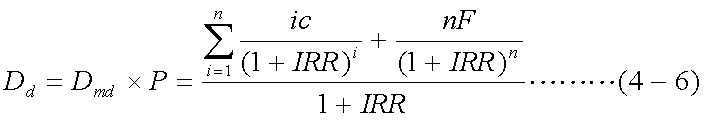
6.コンベクシティー
デュレーションの概念は、債券に関する金利水準(利回り)と現在価格の関係を 分析するために導入された。つまり、ある金利水準の変化に対して現在価格がどれだけ 変化するか、あるいは現在価格が幾らになるかということに注目しているわけである。 ところで、項目2でも述べたように、金利水準に対する現在価格曲線は、常に下に凸で あるから、下のグラフに示すように、デュレーションのみを用いて予測された価格は、 常に過小評価となる問題がある。
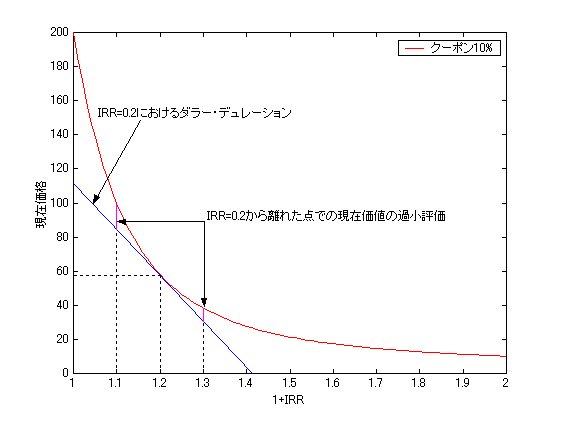
ここで、連続でn回まで微分可能な関数f(x)について、xの値をhだけ変化させた関数の 値f(x+h)は、テイラーの定理により、以下の式のように展開できる(テイラー展開)。
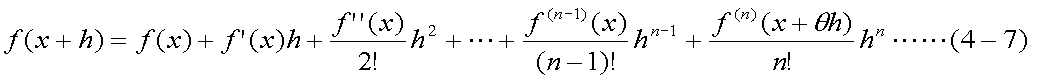
式(4-7)の最後の項は残差項と呼ばれ、f(x+h)の値を導関数の値を用いて近似したとき の言わば誤差である。デュレーションのみを用いて予測する現在価格は、1次導関数の 値のみを用いて近似していることを意味し、残差項をRnと書くと、式(4-8) のようになる。ここで、f'(x)は、ダラー・デュレーションに相当する (符号は逆である)点に留意しよう。
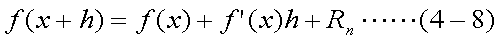
デュレーションのみを用いた価格予測の誤差が大きいのは、式(4-8)において、残差項 Rnが大きいためである。そこで、2次導関数の値まで用いることとし、 以下の式(4-9)のようにして近似する。
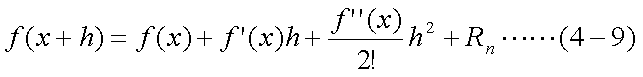
式(4-9)における、f''(x)の値をダラー・コンベクシティーと呼び、式(4-1)をIRRで 2回微分して、即ち式(4-3)をIRRでもう一度微分して求められる。
なお、式(4-10)の両辺を現在価格Pで割り、評価尺度を価格の変化率としたものを 単にコンベクシティーと呼ぶ。これは、以下の式(4-11)で表される。
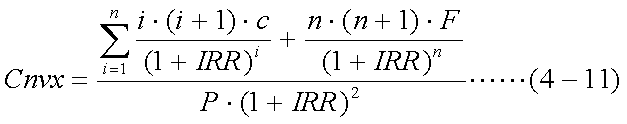
〜例〜
式(4-1)の例について、n=10、F=100、c=3、IRR=2%(1年複利ベース)とする。 この債券について、以下の計算を行ってみよう。まず、現在価格Pは次の通りである。
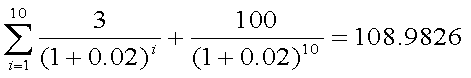
- マコーレーのデュレーション:式(4-2)
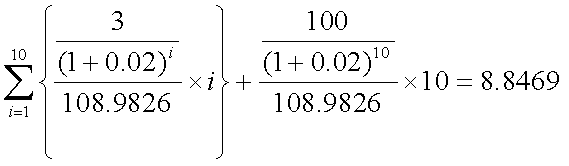
- 修正デュレーション:式(4-5)
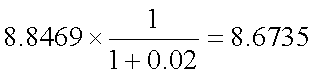
- ダラー・デュレーション:式(4-6)
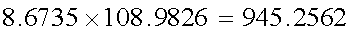
- ダラー・コンベクシティー:式(4-10)
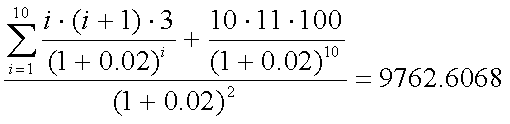
- コンベクシティー:式(4-11)
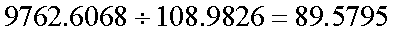
- 利回りが1.5%上昇したときの、債券価格:式(4-1)
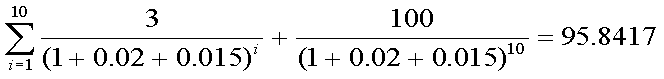
- 利回りが1.5%上昇したときの、デュレーションのみを用いた価格推定値 :式(4-8)
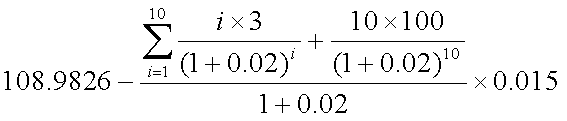
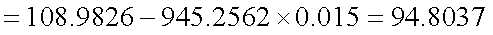
- 利回りが1.5%上昇したときの、デュレーションとコンベクシティーを用いた 価格推定値:式(4-9)
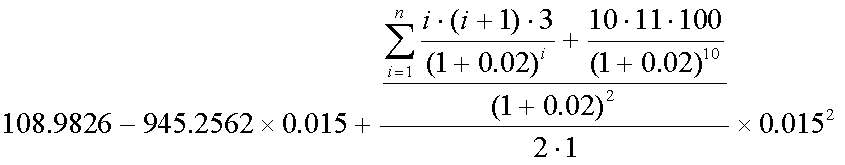
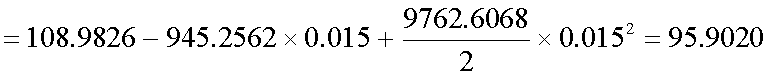
課題(レポートにして次週提出)
式(4-1)の例について、n=15、F=100、IRR=1.819%のとき、クーポンが1.9%、5%、 10%の3種類の債券について、以下の設問に答えなさい。
- それぞれの現在価格を求めなさい。
- それぞれのマコーレーのデュレーションと修正デュレーションを求め、 クーポンの違いに関連付けた考察を行いなさい。
- それぞれのコンベクシティーを求め、クーポンの違いに関連付けた考察を行い なさい。
- それぞれの債券について、利回りが1.5%上昇したときの価格、並びに デュレーションのみを用いた価格推定値、デュレーションとコンベクシティーを 用いた価格推定値を求め、違いを考察しなさい。
- 利回りが上昇したときに、ダラー・デュレーションはどのように変化するか、 考察しなさい。