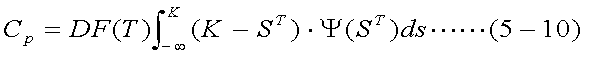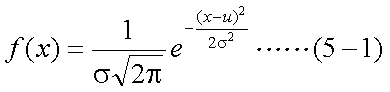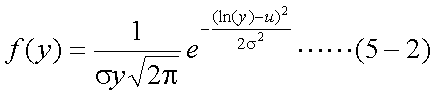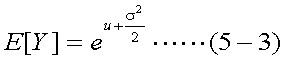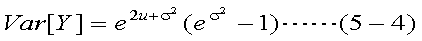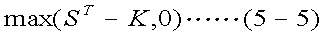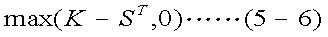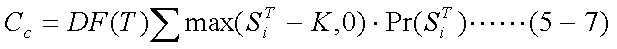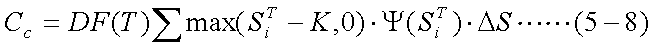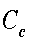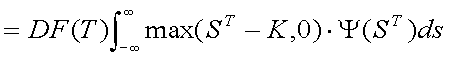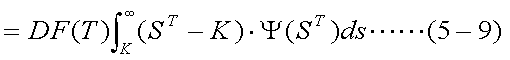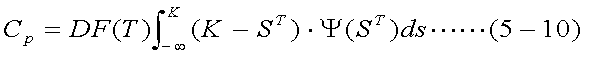1.確率分布
オプションは、将来においてある商品を特定の価格で売買する権利を、現時点に おいて売買する取引であるから、そのオプションの価格(プレミアム)は、 オプションが行使される将来時点において、その商品の価格が幾らになっている 可能性が高いか、といったことから導かれる。
将来の価格は本質的に不確実であるから、現在100万円の商品が、 将来0円になることも、1億円になることも、可能性としてはあり得る。ただし、 そうした極端な価格となる可能性は、例えばこれが105万円になる可能性に比べて 低いであろう。こうした可能性の分布を示すものを確率分布と呼び、正規分布や 対数正規分布がよく使用される。
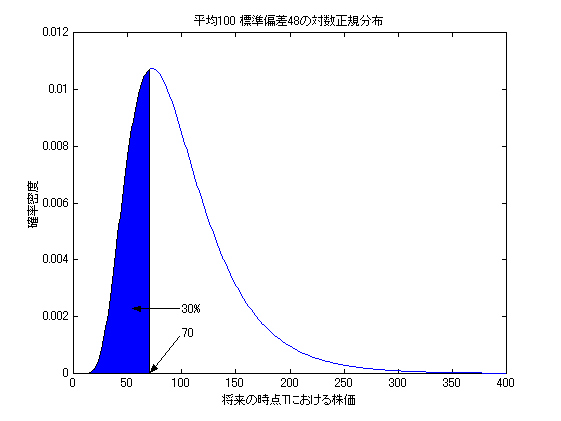
正規分布や対数正規分布の形状は、確率変数(この場合は将来の株価)の平均と 分散(或いは標準偏差)により定まる。ここでは、将来の時点Tにおける株価の平均が ともに100万円とし、70万円以下になる確率がともに30%になるように分散を定めた 正規分布と対数正規分布の例を示す。この例における正規分布では、株価が負となる 領域にも分布範囲がみられるが、実際には株価が0より小さくなることは無いので、 正規分布で価格の分布を仮定するのは現実的ではないと言える。一方、 対数正規分布は、常に0より大きな分布範囲をとるので、こうした問題はない。
図1:将来の株価に正規分布を仮定した例
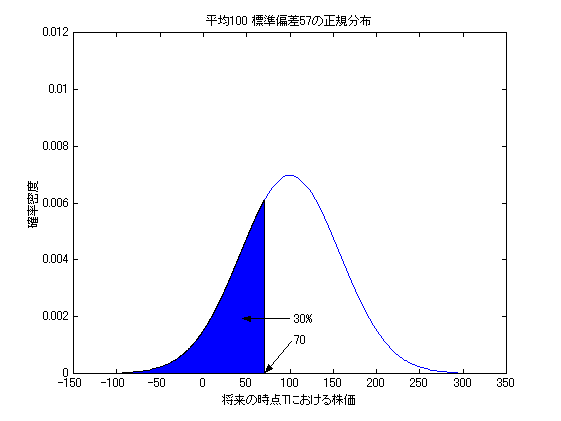
図2:将来の株価に対数正規分布を仮定した例
2.正規分布と対数正規分布
正規分布と対数正規分布は親戚のような関係にあり、正規分布の確率密度関数から 対数正規分布の確率密度関数が導かれる。まず、確率変数Xについて、平均u、 分散σ2の正規分布の確率密度関数は式(5-1)のように与えられ、 u=100、σ=57とすると、図1の曲線が得られる。
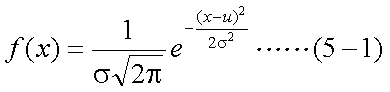
また、確率変数Xが、平均u、分散σ2の正規分布にしたがうとき、 確率変数Y=exは対数正規分布する。この密度関数は、確率変数Xのuとσを 用いて式(5-2)のように与えられ、確率変数Yの平均(E[Y])と分散(Var[Y])は、 それぞれ式(5-3)、式(5-4)のように表される。ここで、E[Y]=100、Var[Y]=48とすると、 図2の曲線が得られる。
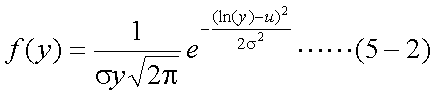
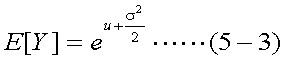
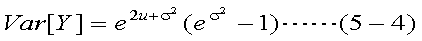
3.オプション・プレミアムの評価式
将来の時点Tにおける株価をSTと表し、オプションの権利行使価格をKと 表すと、コール・オプション・ロングの権利行使日のキャッシュフローは、 ST≧KのときST-K、それ以外のときは0である。 これを式(5-5)のように書き、ペイオフ関数と呼ばれる。同様に、 プット・オプション・ロングのペイオフ関数は、式(5-6)の通りである。
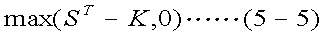
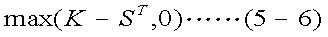
オプションの価格(プレミアム)とは、権利行使日に受け取れるであろう キャッシュフローの期待値の現在価値と考えることができる。ここで、T時点の キャッシュフローを現在価値に換算する係数(ディスカウント・ファクター)を DF(T)とし、T時点に株価がSTi以上、 STi+ΔS以下である確率をPr(STi)と 表すと、コール・オプションのプレミアムCcは、式(5-7)で表される。
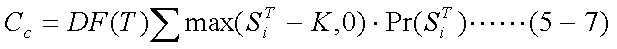
ここで、STiがしたがう確率密度関数を Ψ(STi)とすると、式(5-7)は微小のΔSを用いて、 式(5-8)のように書き直すことができる。
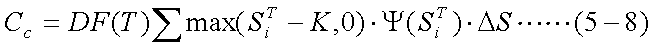
Ψ(STi)は連続であると仮定し、ΔSを小さくして、 ΔS→0の極限を考えると、式(5-8)は以下のように積分の形で書き直すことができ、 これがコール・オプションのプレミアムの評価式となる。 プット・オプションについても 同様に、式(5-10)のようにプレミアムの評価式が得られる。つまり、適切に確率密度 関数Ψ(ST)を仮定することができれば、オプション・プレミアムの 評価が可能となるということである。