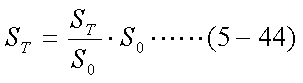
オプション：ブラック＝ショールズ式の考察

１．σの意味

　式(5-42)、式(5-43)に示したブラック＝ショールズ式は、現在の株価S、権利行使価格 K、非危険利子率r、オプション期間T、そしてσを与えることができれば、ヨーロピアン・オプションの価値を計算できることを示している。ここで、σは ボラティリティと呼ばれ、一定期間での変動のしやすさを示す値である。では、具体的にσは何の変動のしやすさであるか考えてみよう。

　まず、将来のT時点の株価をS_Tとおく。ブラック＝ショールズ式では、 S_Tが対数正規分布にしたがうものと仮定し、その確率密度関数は式(5-11)で表された。このとき、ln(S_T)は、平均u、分散σ²の正規分布にしたがうことになる。ところで、現在の株価をS₀とすると、S_T は、以下の式であらわすことができる。

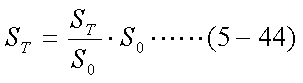
　式(5-44)は、現時点から時点Tまでの株価の伸び率に、現時点の株価をかけたものが T時点の株価であると言っているに過ぎない。ここで、式(5-44)の両辺の対数をとる。

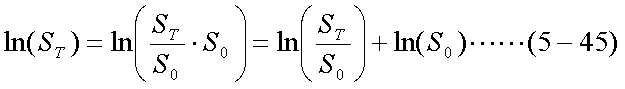
　この式の左辺は前述のように、平均u、分散σ²の正規分布にしたがう。この式の両辺からln(S₀)を引くと、ln(S₀)は定数であるから、以下の式は分布の中心が負側にln(S₀)だけ移動した正規分布、すなわち平均u-ln(S₀)、分散σ²の席分布にしたがう。

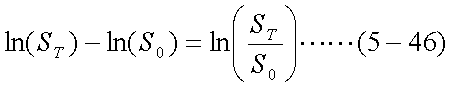
　ちなみに、ln(S_T/S₀)は、連続複利ベースの現時点から時点Tにかけての株価の伸び率である。つまり、期間Tの株価の伸び率が、平均 u-ln(S₀)、分散σ²の正規分布にしたがうということである。さらに、1年間のσをσ_anとすると、式(5-40)の関係がある。よって、ブラック＝ショールズ式(5-42)、及び式(5-43)のσ_anには、期間1年間での株価の伸び率の標準偏差を代入すればよい、ということになる。

２．標準正規分布の累積密度関数の値

　ブラック＝ショールズ式における関数N(x)は、標準正規分布の確率密度関数をある範囲で積分したものであるので、標準正規分布の累積確率密度関数と呼ばれる。この値は、数値積分により求めることができるが、統計学の本に掲載されている数表や Excelの関数（NORMSDIST）により簡単に得ることもできる。また、その両方が手元に無いときであっても、以下の近似式により電卓のみで計算することも可能である。

x≧0のとき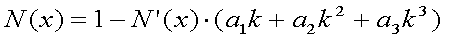
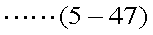x＜0のとき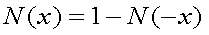

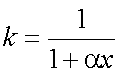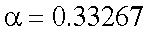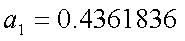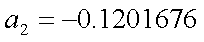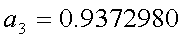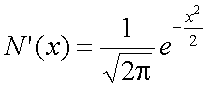
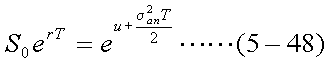
ただし、

、

近似式の出典：M. Abramowitz and I. Stegun, "Handbook of Mathematical Functions" New York: Dover Publications, 1972

３．株価の伸び率の確率分布

　前述のように、期間Tの株価の伸び率は、平均u-ln(S₀)、分散σ²の正規分布にしたがう。ここで、uは依然として不明確な値であるので、このままでは株価の伸び率の具体的な確率分布を得ることはできない。そこで、現在の株価とそのT時点における期待値には、式(5-35)の関係があることを思い出し、期間1年間での株価の伸び率の標準偏差をσ_anとして書き直すと、次の式が得られる。なお、rは非危険利子率（期間Tの年率金利）である。

　これをln(S₀)について解くと、式(5-49)が得られる。

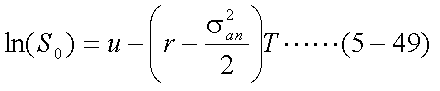
　よって、期間Tの株価の伸び率がしたがう正規分布の平均u-ln(S₀)は、次のようになる。

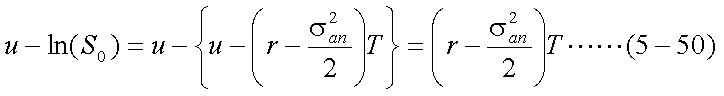
　以上をまとめて、期間Tの株価の伸び率は、以下の正規分布にしたがう。

平均	分散

４．ブラック＝ショールズ式による計算例

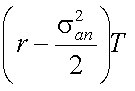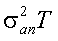現在の株価	100万円
権利行使価格	95万円
非危険利子率	3％
ボラティリティ	10％
オプション期間	半年

　上記の条件のヨーロピアン・コール・オプションの価格（C）は、以下のようにして計算することができる。

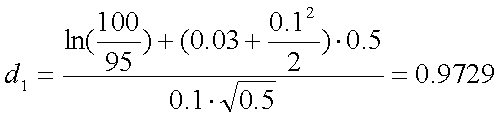
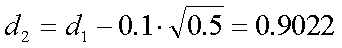
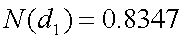
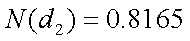
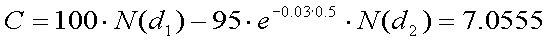
　同様に、ヨーロピアン・プット・オプションの価格（P）は、以下の通りである。

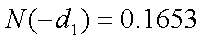
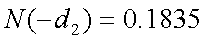
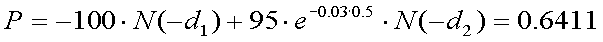
　以上より、コール・オプションの価格は7万555円、プット・オプションの価格は 6411円であることが分かる。

課題（レポートにして次週提出）

　次の条件の、ヨーロピアン・コール・オプションとヨーロピアン・プット・オプションの価格を、それぞれ計算しなさい。

問題番号	1	2	3	4	5	6	7
現在の株価	105万円	105万円	105万円	105万円	105万円	105万円	105万円
権利行使価格	95万円	95万円	95万円	95万円	95万円	95万円	95万円
非危険利子率	5％	5％	5％	4％	6％	5％	5％
ボラティリティ	20％	20％	20％	20％	20％	10％	30％
オプション期間	3ヶ月	半年	1年	半年	半年	半年	半年