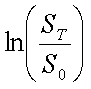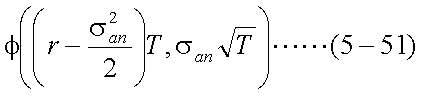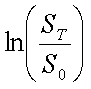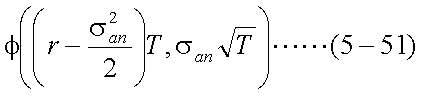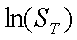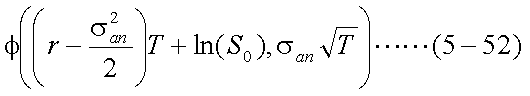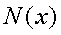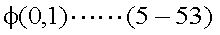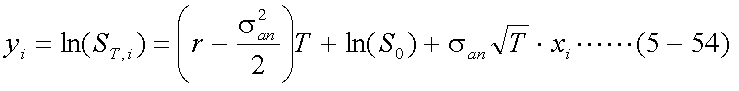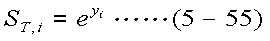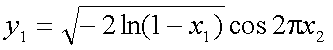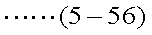1.モンテカルロ・シミュレーション
ヨーロピアン・オプションの一般的な評価式は、式(5-9)、式(5-10)の通りであり、 これは権利行使時点での原資産がとり得る価格について分布が仮定できれば、 そのオプションの価値が評価できることを意味している。ブラック=ショールズ式は、 これが対数正規分布にしたがうことを仮定し、容易に計算可能な形式にまで、 式の展開を進めたものである。
この分布形状を示す確率密度関数が複雑な場合や、確率変数が複数ある場合には、 解析的に(言わば、紙と鉛筆と電卓で)計算することが困難となるため、数値的な 手法を用いる必要が生じる。すなわち、権利行使時点における原資産の具体的な 価格を、乱数を用いて無数に発生させ、結果として生じる全てのペイオフの平均値を 求めるようなコンピュータ・シミュレーションを行うのである。
こうしたシミュレーションをモンテカルロ法と呼ぶが、仮定された分布にしたがう 乱数を適切に発生させることができれば、複雑なオプションにも柔軟に適用できる ということが最大の利点である。ただし、計算精度を向上させるためには、膨大な 回数の計算を繰り返さなければならず、高速なコンピュータを用いても、結果を得る のに時間がかかるという問題はある。
ここでは、ヨーロピアン・オプションの価値を、モンテカルロ・シミュレーション を用いて評価する方法を学び、ブラック=ショールズ式を用いた場合と同様な結果が 得られることを確認する。なお、通常は解析的なアプローチが可能な場合は、 できるだけそちらを選択すべきである。というのは、正確さの点で、シミュレーション により得られた解は、解析解に劣ると言わざるを得ないためである。ここでは、 モンテカルロ・シミュレーションの手法を理解するために、あえて簡単なオプション 評価に適用しているに過ぎない。
2.STの分布
将来T時点の株価STは対数正規分布にしたがうと仮定しているが、 具体的な分布形状は、その対数であるln(ST)がしたがう正規分布の、 平均と分散により定まる。そこで、期間Tの株価の伸び率は、以下のような正規分布に したがうことを思い出そう。
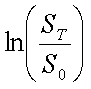 |
〜 |
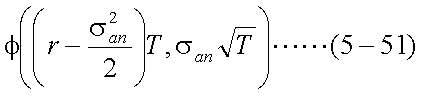 |
上記正規分布について、分布の中心を正方向にln(S0)だけ移動する。 正規分布は平均を中心に対称なので、平均値がその分だけ変化する。感覚的には、 上式(5-51)の両辺に、ln(S0)を加えるイメージである。その結果、 将来時点Tの株価の対数ln(ST)が、以下のような正規分布にしたがう。
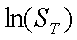 |
〜 |
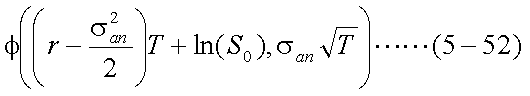 |
よって、式(5-52)で示される分布にしたがう乱数を生成すれば、時点Tにおける株価 のサンプルが得られることが分かる。通常は、式(5-52)にしたがう乱数を直接生成する のではなく、式(5-53)のような標準正規分布にしたがう乱数xを生成し、 各xiについて式(5-54)に示す変換を行って、STのサンプルを 得る。
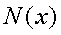 |
〜 |
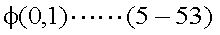 |
あるT時点における株価の対数のサンプルを、式(5-54)に示すようにyi とすると、株価のサンプルは式(5-55)により得られる。
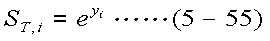
3.標準正規分布にしたがう乱数の生成法
0以上1未満で一様に分布する2つの乱数x1、x2があるとき、 次の2式により生成される2つの数y1、y2は互いに独立な 標準正規分布にしたがう乱数となる。これは、Box-Muller法、あるいは 極座標法と呼ばれ、標準正規分布にしたがう乱数を生成するのに、 最もよく用いられるものの1つである。Box-Muller法の考え方に関する説明は、 ここでは割愛する。また、一様分布乱数の生成アルゴリズムに関しては、 次回とりあげる。
4.Excelによる実装例
Excelでは、0以上1未満の一様乱数を生成するのに、関数RAND()が使用できる。 この関数で使用されているアルゴリズムや生成される乱数の性能は不明であるが、 ここでは、とりあえずこの関数を使用して、ヨーロピアン・オプションの評価を 行うためのモンテカルロ・シミュレーションを、Excel上で行う方法について 紹介する。その手順は以下の通り。
- 現在の株価、権利行使価格、非危険利子率、ボラティリティ、オプション期間 といった各種パラメータは、特定のセルに入力しておき、各計算式ではこれらを 絶対参照で使用するようにする。
- 関数RAND()を使用して、1つの行に0以上1未満の2つの一様乱数を生成する (x1、x2)。
- 式(5-56)のBox-Mullerh法を用いて、上記2つの一様乱数から、1つの行に2つの 標準正規分布にしたがう乱数を得る(y1、y2)。
- 式(5-54)を用いて、上記2つの標準正規分布にしたがう乱数から、1つの行に 2つの時点Tにおける株価の対数のサンプルを得る。
- 式(5-55)を用いて、株価の対数を株価に変換する。
- 2つの株価のサンプルについて、権利行使価格との差を計算し、コール・ オプション、プット・オプションそれぞれについて、2つのペイオフのサンプルを 得る。
- 以上で1行に入力した全ての式を、他の行にコピーする。1行で2つのサンプルを 得ることができるので、1万回の計算を行いたい場合には5千行にコピーすれば よい。Excelの計算効率を考えると、現実的なのは5万回(2万5千行)程度まで である。
- コール・オプション、プット・オプションそれぞれについて、関数AVERAGE()を 用いて、ペイオフの平均値を計算する。
- 上記平均値を、現在価値に直したものが、オプション・プレミアムの評価値 である。
〜Excelでの実装例〜