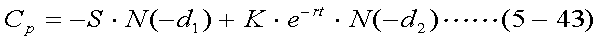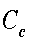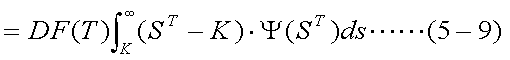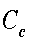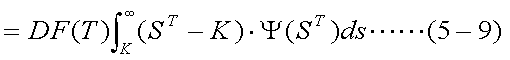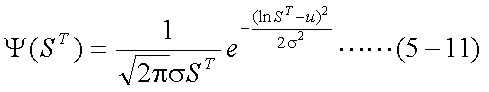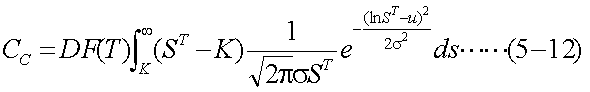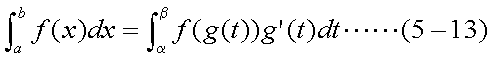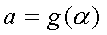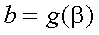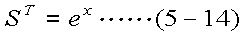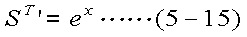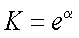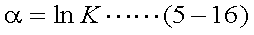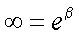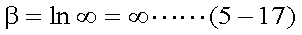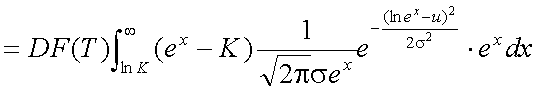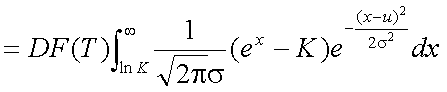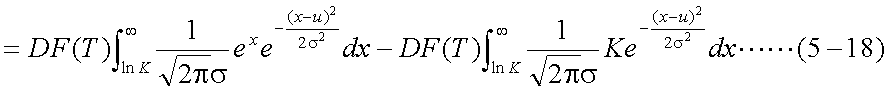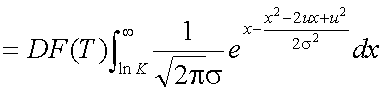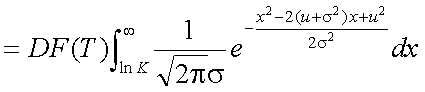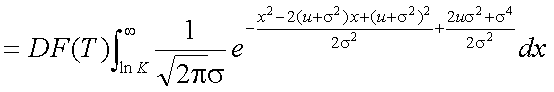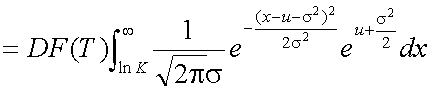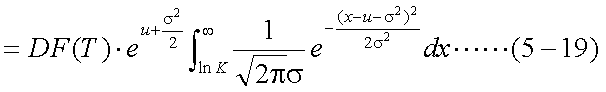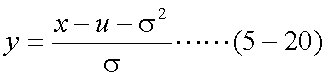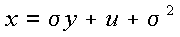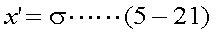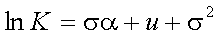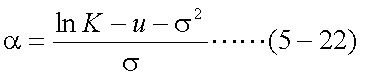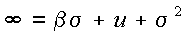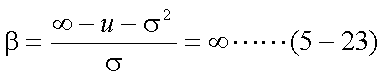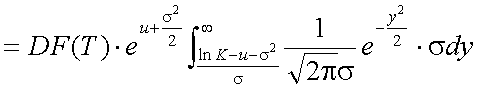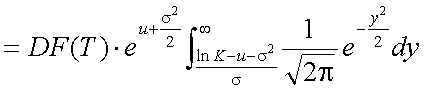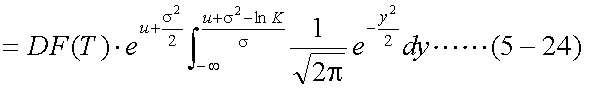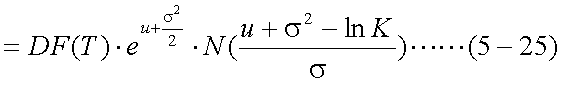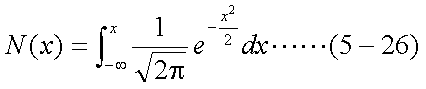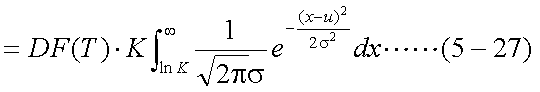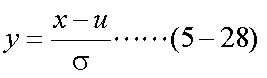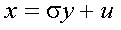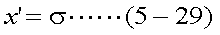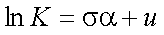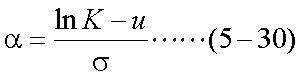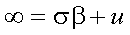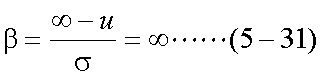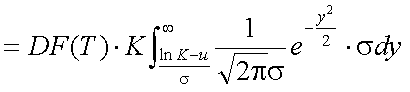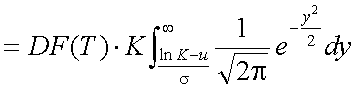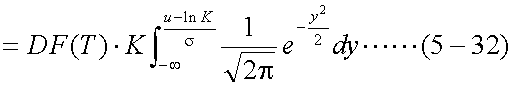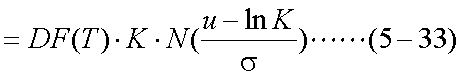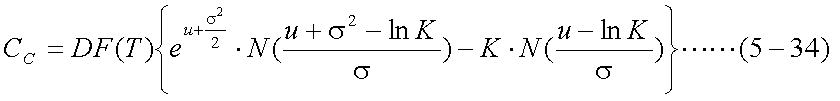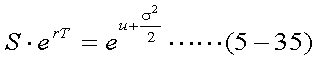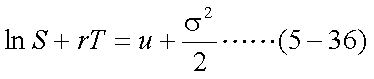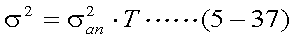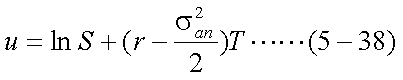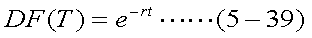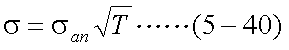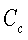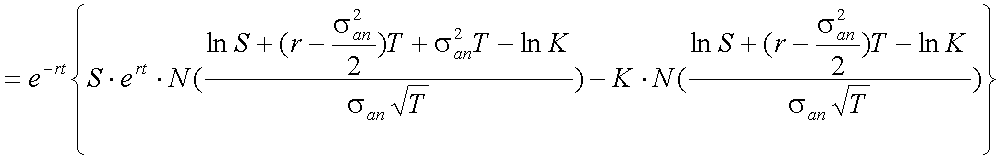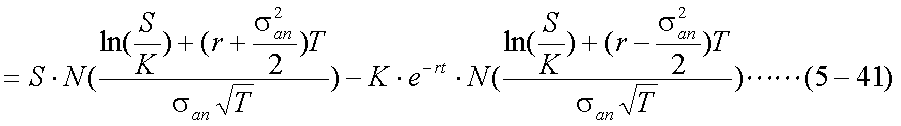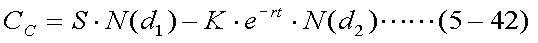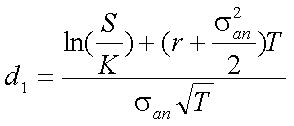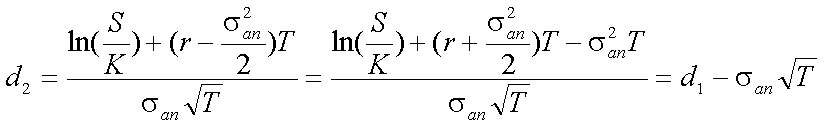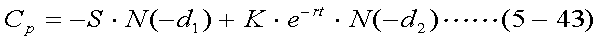オプション：ブラック＝ショールズ式の導出

１．ブラック＝ショールズ式とは？

　1973年のJournal of Political Economy（Vol.81 pp.637-654）において、 Fischer BlackとMyron Scholesは、「The Pricing of Options and Corporate Liabilities」と題した論文を発表した。この論文は、オプションの理論価格 を評価する公式を発表したもので、それ以前のオプション価格が市場における需給により形成されていたことを考えると、まさに画期的な発見であった。本論文において導かれている公式は、ブラック＝ショールズ式と呼ばれ、以降の研究に多大な影響を与えている。
　残念ながら、Fischer Blackは1995年に死去したが、Myron Scholesは、ブラック＝ショールズ式の正しさを証明する論文を発表したRobert C. Mertonとともに、 1997年のノーベル経済学賞を受賞している。
　BlackとScholesのアプローチは、株式の価格変動がしたがう確率過程を仮定（幾何ブラウン運動）し、他商品との裁定機会がないところから導かれる偏微分方程式を解くというものであった。ここでは、偏微分方程式の解説を省略する目的で（現時点では学んでないだろうからね）、前項で導いた概念的なオプション・プレミアムの評価式に、将来T時点の株価の確率密度関数 Ψ(S^T)を直接的に仮定する方法で、ブラック＝ショールズ式を導出するアプローチをとる。

２．ヨーロピアン・コール・オプションのブラック＝ショールズ式

第1段階：将来T時点の株価の確率密度関数の仮定

　前項で示したように、コール・オプションのプレミアムは、式(5-9)で表される。この式が示すのは、将来T時点の株価がしたがう確率密度関数を適切に仮定すれば、オプション・プレミアムの評価が可能であるということである。

　ここで、将来T時点の株価が前項で解説した対数正規分布にしたがうものと仮定する。対数正規分布の確率密度関数は、正規分布より導かれるから、正規分布の平均uと分散σ²を仮定する必要がある。この平均と分散が持つ意味については、次項で解説するものとし、ここでは将来T時点の株価がしたがう確率密度関数を、式(5-11)のような対数正規分布として仮定する。その結果、式(5-9)は式(5-12)のようになる。

第2段階：置換積分による式の展開

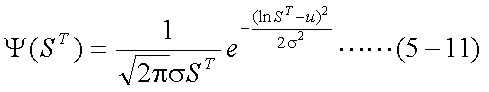
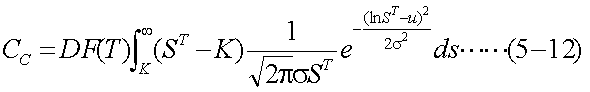
　式(5-12)をそのまま計算してもよいが、より簡単に計算できるようにするために（ブラック＝ショールズ式と同じにするために）、これを展開して行が、ここでは、置換積分という数学的テクニックを使用する。これは、関数f(x)の積分において、ある単調増加関数g(t)により、x=g(t)と置き換えて積分することである。


ただし、

　ここで、S^Tを式(5-14)のように置く。このとき、その導関数 S^T'は式(5-15) であり、積分範囲は式(5-16)、式(5-17)となる。

	より、
	より、

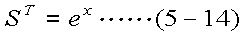
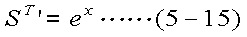
　以上から、式(5-12)は、式(5-18)のように、展開することができる。

第3段階：式(5-18)第1項の整理

　式(5-18)の第1項を整理して、簡単に計算可能な形式とする。問題は積分の部分であるが、標準正規分布（平均0、分散1の正規分布）の密度関数の積分値であれば、統計関連書籍の数表や、多項近似式により簡単に計算可能である。そこで、目標としては、積分の部分を標準正規分布の密度関数の積分のみにし、他の部分を外に出すということになる。まず、第1項は式(5-19)の形に変形できる。

第1項

　式(5-19)はxの関数であるが、式(5-20)のような変数変換を行ってyの関数とし、置換積分を行う。ここで、置換積分における導関数は式(5-21)、積分範囲は式(5-22)、式(5-23)となる。

より、

	より、
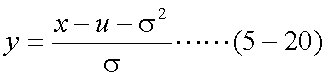
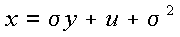	より、

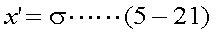　以上式(5-20)～式(5-23)を用いて、式(5-19)を書き換えると、以下の式(5-24)が得られる。

第1項

　式(5-24)の積分の中は、まさに標準正規分布の確率密度関数となっているので、これをN(x)と表すと、式(5-24)は式(5-25)のようになる。

第1項

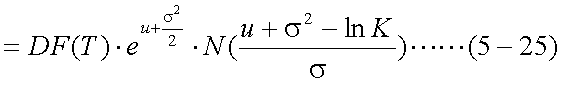ただし、

第4段階：式(5-18)第2項の整理

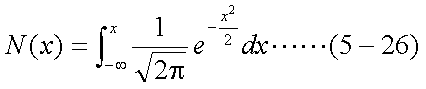　第1項と同様に、式(5-18)の第2項についても整理して、簡単に計算可能な形式とする。この場合も、問題となるのは積分の部分であり、第1項と同様、これを標準正規分布の密度関数の積分のみとする方針で整理して行く。まず、式(5-18)の第2項は以下の式(5-27)のようになる。

第2項

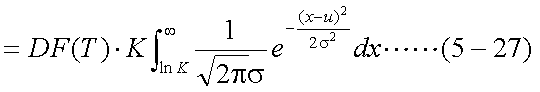　ここで、式(5-28)のような変数変換を行い、置換積分を行う。ここで、置換積分における導関数は式(5-29)、積分範囲は式(5-30)、式(5-31)となる。

より、

	より、
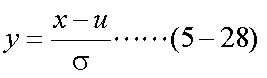
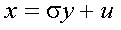	より、

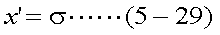　以上式(5-28)～式(5-31)を用いて、式(5-27)を書き換えると、以下の式(5-32)が得られる。

第2項

　式(5-32)の積分の中は、まさに標準正規分布の確率密度関数であるので、第1項の場合と同様に、これをN(x)と表すと、式(5-32)は式(5-33)のようになる。

第2項

第5段階：ブラック＝ショールズ式の導出

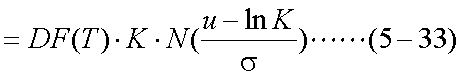　式(5-18)、式(5-25)、式(5-33)から、ヨーロピアン・コール・オプションのプレミアムは、以下の式(5-34)で表される。

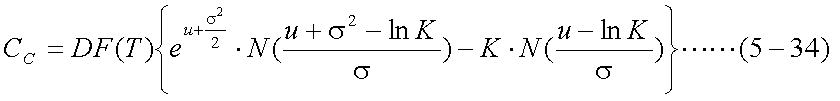
　式(5-34)によると、将来時点Tにおける株価が従う確率密度関数、即ち式(5-11)におけるuとσが得られれば、ヨーロピアン・コール・オプションのプレミアムが計算できる。ここで、将来時点Tの株価が対数正規分布にしたがうと仮定したことを思い出そう。このとき、将来時点Tの株価の期待値（平均値）は、現在その株を購入するのに必要な資金を、安全資産に投資した場合のT時点における将来価値と等しくなければならない。なぜなら、安全資産に投資した将来価値の方が高ければ、株に投資する人は居ないはずだし、逆に株価の期待値のほうが高ければ、皆が株に投資するはずだからである。
　よって、安全資産の収益率（金利水準）をr（連続複利ベース）とし、現在の株価をSとすると、以下の関係が成り立つ。なお、右辺は対数正規分布の平均である（前項参照のこと）。

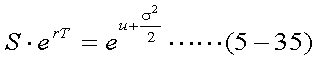
　式(5-35)について、両辺の対数をとると、式(5-36)のようになる。

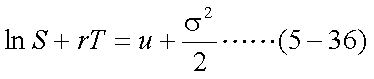
　また、1年間のσをσ_anと表すと、式(5-37)の関係がある。

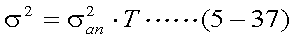
　式(5-36)を式(5-37)を用いて書き直すと、式(5-38)のようになる。

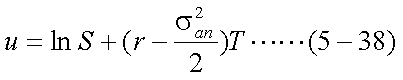
　さらに、T時点のキャッシュフローを現在価値に換算する係数（ディスカウント・ファクター）DF(T)は、安全資産の利回りがrであるから、式(5-39)のようになる。

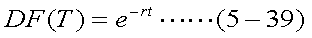
　なお、式(5-34)におけるσは、式(5-37)より以下のようになる。

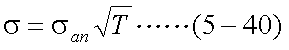
　式(5-34)を、式(5-35)、および式(5-37)～式(5-40)を用いて書き直すと、式(5-41)が得られる。

　上の式(5-41)が、ヨーロピアン・コール・オプションのプレミアムを評価するブラック＝ショールズ式である。この式は、標準正規分布の確率密度関数N(x)の中を、それぞれd₁、d₂と置いて、以下のように表記されることが多い。

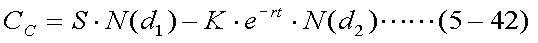
ただし、

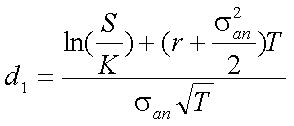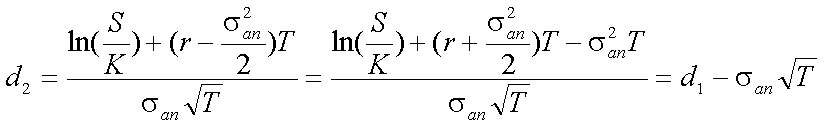課題（レポートにして次週提出）

ヨーロピアン・プット・オプションのプレミアム評価式は、式(5-42)における d₁とd₂を用いて、以下のように表される。本項での方法にしたがって、以下の式が導かれることを示せ。